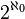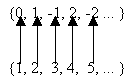Y así

Hoy es una de esas tardes poco productivas. Te levantas a las 17:23 después de haber trasnochado - actividad que nunca me ha llamado especialmente la atención - y por puro instinto de supervivencia, te fríes unas pechugas de pollo que acompañas de queso y pan, y arroz con leche de postre.

¿Sales? Nadie sale. ¿Lees? No tienes ganas. ¿Vas al cine? ¿sólo? Pues hale, en casa, sin hacer nada. Y lo peor es que hay una frase que te da vueltas en la cabeza: "Sólo se aburren los tontos, como debe usted saber..."

Como yo no soy tonto, voy a dar una vuelta, a ver qué se cuece.

Contando pollos (III parte)

Tras una breve espera reanudamos nuestra serie de artículos sobre conjuntos infinitos, dispuestos a dar respuesta a las preguntas que faltan. En la anterior entrada prometimos dar una prueba de que el orden de infinitud de los números reales es efectivamente mayor que el de los números naturales - si recordáis las anteriores explicaciones, probar esto implicaría probar también que el orden de infinitud de los reales es mayor que el de los enteros y los racionales, puesto que el cardinal transfinito de todos estos conjuntos es, como ya vimos, el mismo (). 

Vamos a dar unas pequeñas explicaciones preliminares, para pasar luego a abordar el problema con mayor seguridad. El conjunto de los números reales es, expresado de una manera sencilla, el formado por el conjunto de los números racionales (fracciones) y el conjunto de los números irracionales. Éstos últimos se caracterizan por tener infinitas cifras decimales que van sucediéndose de manera no periódica; los ejemplos más famosos son, como quizá conozcáis, el número π ("pi"), el número e ("e") o el número Φ ("número áureo"). La característica que diferencia a los números irracionales de los racionales es que no podemos dar una pauta que nos permita conocer la sucesión de sus cifras decimales, cosa que sí ocurre con los segundos.

¿Cuál es la esencia de la prueba?

Möbius band, M.C. Escher

 Vamos a llevar hasta el extremo nuestra analogía de las filas de pollos. Si lo que pretendemos es mostrar que un conjunto tiene un orden de infinitud mayor que otro, lo que en realidad pretendemos es ver que al emparejar los pollos de cada familia y hacerles desfilar por la puertecita del corral, al menos uno va a quedar descolgado y perdido. Por lo tanto y en buena lógica, lo que vamos a hacer es suponer que todos están ya emparejados, para luego ver que esto es imposible. Vamos a ello:

Supongamos que tenemos una lista numerada con todos los números reales. Esto equivale a emparejar cada número natural con un número real (el orden de aparición nos da igual). Para simplificar la prueba, vamos a suponer que la lista numerada contiene los números reales del 0 al 1 (es fácil probar que el orden de infinitud de este intervalo es equivalente al de toda la recta real, cosa que no demostraremos).

Así pues, una posible lista sería la que sigue:

1. 0.132245677538323..........................
2. 0.573839728947238..........................
3. 0.683447384579397..........................
4. 0.093993828273833.........................

etcétera. Ahora vamos a fijar nuestra atención en la cifra decimal correspondiente a la posición de cada número en la lista. Por ejemplo, nos fijaremos en la primera cifra decimal del número real que ocupa la posición 1, en la segunda cifra decimal del número real que ocupa la posición 2, y así sucesivamente. Vamos a construir en base a ello un número real tan rematadamente enrevesado que será imposible que esté en la lista.

**** Rogamos a los lectores mantengan la serenidad y lean con calma;

 ni el número es tan enrevesado, ni el autor pretende un holocausto cerebral **** 

La pequeña regla que vamos a utilizar será la siguiente: para conocer la cifra decimal que ocupa el lugar p de nuestro número, observaremos el número que ocupa el lugar p en nuestra lista y nos fijaremos en su p-ésima cifra decimal. Sea n el valor de esta cifra, entonces la cifra de nuestro número será, precisamente, n+1 (en el caso de que el valor de n sea 9 , la cifra de nuestro número será 0).

Vamos a clarificar esta regla con un ejemplo en base a nuestra querida lista: ¿cuál será la primera cifra decimal de nuestro número enrevesado? Viendo la primera cifra decimal del primer número de la lista, esto es, 1, tenemos que la primera cifra de nuestro número enrevesado será 1 + 1 = 2. Sencillo, ¿no?

número enrevesado = x = 0.2.................................

¿cuál será la segunda cifra decimal de nuestro número enrevesado? Viendo la segunda cifra decimal del segundo número de la lista, es decir, 7, tenemos que la segunda cifra de nuestro número enrevesado será 7 + 1 = 8.

número enrevesado = x = 0.28.............................

Y así sucesivamente, quedando x = 0.2840..............................

Ahora viene el golpe de gracia: ¿puede nuestra lista contener al número x?  Preguntémonos lo siguiente, que es lo mismo; ¿puede nuestro número x encontrarse en un lugar de nuestra lista? o bien, dicho de otra manera, ¿puede estar nuestro número x en el lugar m de la lista, donde m es cualquier número natural?

Es claro que esto no puede ocurrir ya que, tal y como lo hemos construido, nuestro número difiere del que ocupa el lugar m precisamente en la m-ésima cifra decimal. Para verlo más concretamente: nuestro número no puede estar en el lugar "1" de la lista, puesto que, como ya observamos, la 1ª cifra del número x y la 1ª cifra del número 1 de la lista ya son distintas. Vemos con claridad que lo mismo le sucede con el 2º número de la lista, con el 3º, el 4º, y así con todos los que quiera haber.

Nuestro número x es el pollo que queda descolgado, y por tanto hemos visto que el conjunto de los números reales es necesariamente de orden mayor que el conjunto de los números naturales. Más concretamente, el orden de infinitud de los números reales es , ya podéis ver que este corral entra dentro de la categoría de lo "bestia".

Los matemáticos tienen fama de parcos en palabras, principalmente porque la mayoría de ellos piensa que no es necesario añadir más cuando ya se ha demostrado algo. En este caso el artículo se ha alargado más de lo que yo pensaba, y creo que por deferencia hacia el paciente lector, vamos a acabar sin mayor esfuerzo adicional. Queda en el aire la respuesta a la pregunta ¿hay más números pares positivos que naturales? Sirva como aliciente para aquellos que se interesen por los emparejamientos de pollos. Os dejo con un recuerdo del infinito...

Volando entre las columnas

Es extraño cómo funciona la memoria; al final, la mayor parte de las vivencias que uno cree recordar son tan sólo construcciones, en gran medida constituidas por elementos ficticios, que forman escenas inmóviles o, en ocasiones, secuencias a cámara lenta. Entre mis recuerdos más queridos de los años de aprendizaje en el instituto sobresale una imagen de sus majestuosos pasillos, avanzando lentamente entre el juego de luces y sombras formado por los numerosos ventanales. Todavía soy capaz de sentir aquella atmósfera unas veces deslumbrante, otras veces tenuamente velada, como con el tiempo suspendido entre las inmóviles motas de polvo atrapadas por el aire. El silencio y la calma presiden, invisibles, todas esas imágenes. Tan sólo el ruido rítmico de mis pisadas caminando pausadamente se atreve a desafiarles. Las paredes, embaldosadas de amarillo y luz, parecen contener la respiración... Grandes cuadros, mapas coloniales, napoleónicos y romanos, tubos de ensayo, probetas y artilugios encerrados en sus vitrinas; todos son presa de la eternidad suspensa, centros de gravedad de las innumerables motas de polvo, convertidas para ellos en minúsculos satélites. Una puerta se abre tímidamente, a lo lejos, para acto seguido cerrarse con un suave quejido, como un reproche.

¿Cómo olvidar aquellos susurros del pasillo de dirección, aquella mezcla de papel, mármol, café, fotocopias y maderas nobles? Un breve instante de calma y lejanas conversaciones, perdidos sus ecos hacia las cumbres del elevado techo, enmarcan la solemnidad del templo. Un teléfono suena a lo lejos. Bajo despacio por la escalera principal, que es digna de reyes, y en su día lo fue de tiranos, como atestiguan las elocuentes paredes en escala de grises. Un escudo de otros tiempos me observa luminoso, con un destello solar fugaz e iracundo. Las gruesas paredes se yerguen, implacables, a medida que desciendo. Dejo atrás las motas de polvo, abro una puerta enmarcada por un noble portón, y salgo a la luz del día. Es un verano radiante, y todo ha quedado atrás. Suena el murmullo de la vida en cada rincón, pero mi corazón guarda todavía aquel silencio sagrado.

Todas las vivencias de mi época de estudiante se encuentran diluidas en la figura de aquel  solemne coloso. Los rostros amigos se agolpan en la memoria, acompañándome por cada uno de los rincones del gigante de piedra, sonrientes y afables como los recuerdos que se alejan... Recuerdo el verde de las mesas y el amarillo parcheado de las paredes, el gris de los techos y los marcos de las puertas, y aquel blanco de la virgen de escayola inmaculada, testigo de otros tiempos, aunque benevolente y comprensivo en su gesto.  La vetusta escalera de la biblioteca, con sus quisquillosos rugidos, pasa fugazmente ante mis ojos, arrebatada por la campana del recreo. Todavía me sobresalta al recordarlo el grito desgarrado del timbre, autoritario al principio de las clases y revolucionario a su final. Algo  indefinido sigue vibrando en aquella campana locuaz y saltarina... Repentinamente me viene a la mente, en terrible contraste, el recuerdo moribundo y lóbrego del viejo mecanismo del reloj principal, asombrado de, por fin, volver a mirar un rostro joven. Aquel vetusto reloj por siempre detenido es el timón del barco de piedra, la esencia y la mirada del  gigante de tez arenisca y cabellos rojizos de teja. Lo que nadie sabe es lo que esconden sus pupilas de aguja, tesoro guardado en el fondo de su alma candada, su mecanismo seco y suspendido, el espíritu bajo las telas de araña del tejado. En la azotea de las trampas de paloma me sentí el marinero más orgulloso de esa nave indestructible, con la antigua capilla a mis pies como un ilustre castillo de proa, y el altivo mástil de hierro de la torrecita puntiaguda, sembrada de azul y gris, a mis espaldas.

Ayer volví a ver el Instituto. Se oían las voces a lo lejos y, en mi interior, yo contemplaba la calma de su espíritu y escuchaba aquel eterno silencio sagrado...

Contando pollos (II parte)

Hacia el final de la primera entrada dedicada a los conjuntos infinitos nos planteábamos una serie de preguntas acerca de conjuntos distintos de los números naturales y enteros. Si nos fijásemos  por ejemplo en el conjunto de los números racionales, denotados por , observaríamos una propiedad curiosa y fácil de constatar: que entre dos números racionales siempre  podemos encontrar infinitos números racionales.

Quizás estemos yendo demasiado deprisa: para aquellos que deseen refrescar su memoria, los números racionales son aquellos de la forma  p/q , donde p y q son números enteros. Es decir, nos estamos refiriendo a las fracciones, también denominadas quebrados, de aquellos años queridos y lejanos de 2º de la E.S.O.

Como es de rigor entre los matemáticos, vamos a ofrecer una pequeña demostración, estudiada en 1º de carrera, que prueba el resultado anterior (tranquilidad, es casi inmediata):

• Entre dos números racionales existen infinitos números racionales:

Demostración: Sean p y q dos números racionales. Supongamos por ejemplo que fuera  
p > q (Si ocurriese lo contrario, la prueba sería la misma).  
Tenemos que:

Esto es, tomamos el punto medio del segmento de recta determinado por p y q, que necesariamente cumple la relación señalada. Este punto medio es, como se ve claramente, otro número racional, y reiterando este argumento podemos construir tantos números racionales como queramos entre p y q.   c.q.d.

Visto esto, vamos a ver que el orden de infinitud del conjunto de los números racionales es el mismo que el de los números naturales, es decir, usando la terminología técnica del artículo anterior, que podemos emparejar las filas de ambos conjuntos de pollos sin que ninguno quede descolgado.

Alguien podría decir: "Está bien, podría aceptar que los conjuntos de los números enteros y los números naturales tienen el mismo orden de infinitud, aunque me resulta raro que pueda ocurrir semejante cosa. Pero, señor mío, ¿¿cómo puede sostener seriamente que el conjunto de los números racionales pueda ser igual de "grande" que el de los naturales si, por ejemplo, entre el 1 y el 2 ya tenemos infinitos?? Está usted sin duda intentando embaucarme".

Es natural que alguien pensara algo así, y para eso se hicieron las demostraciones. Como vimos en el artículo anterior, se trata de dar una regla concreta que permita emparejar los elementos de ambos conjuntos mediante correspondencia biyectiva (emparejar las dos filas de pollos que desfilan, sin que sobre ni falte ninguno). En este caso apelaremos de nuevo al genio de Cantor para que nos muestre cómo podemos emparejar debidamente ambos conjuntos. Se trata en este caso del llamado argumento diagonal, que podemos explicar de manera gráfica. Veamos la siguiente imagen:

Lo que hemos hecho ha sido ordenar todos los posibles números racionales positivos, de manera que podamos recorrerlos todos sin temor a dejarnos ninguno por el camino. De esta forma, y siguiendo el trazado recorrido por la flecha, a cada número racional le asociamos un número natural,  quedando así todos emparejados. Como puede observarse, el por qué de la denominación del razonamiento es fácil de deducir. El hecho de que haya fracciones equivalentes no supone ningún problema: podemos tachar todas las demás una vez que tengamos una de ellas, y la flecha sigue el mismo recorrido "saltando por encima" de esa fracción. Por ejemplo, el 2/2 es equivalente al 1/1, pero podemos tachar el 2/2, el 3/3,  ... etc sin que ello suponga ninguna alteración en los emparejamientos (simplemente, no lo contamos). De manera análoga podemos incluir en esta numeración a las fracciones negativas y el número 0, con lo cual nos quedan las dos filas de pollos emparejadas por correspondencia biyectiva. En suma, el conjunto de los números naturales y el conjunto de los números racionales tienen el mismo cardinal de infinitud que, como ya señalamos en el artículo anterior, es .

¿Sorprendidos? El que no podamos contar los pollos no es obstáculo para que sepamos quién tiene más, como ya hemos explicado... La barrera más complicada de superar es la de la intuición surgida de la experiencia cotidiana. 

Me da la sensación de que ha sido mucha matemática por hoy... ¡A fin de cuentas estamos de vacaciones! En el siguiente y último artículo veremos que, finalmente, existe un conjunto infinito de mayor orden que el de los números naturales (¿ya comenzabais a dudarlo?), y éste es el conjunto de los números reales, denotado por .


Para finalizar (no todo va a ser trabajo) os dejo con un interesante vídeo en el que aparece uno de las piezas más divertidas de la obra de J.S. Bach: se trata del llamado "Canon Cancrizans", (Crab Canon, o  Canon Cangrejo). La peculiaridad de este canon, que aparece explicada visualmente, radica en que la línea melódica del acompañamiento es exactamente la línea melódica principal, pero ejecutada de derecha a izquierda. Además, el autor expone una curiosa animación que muestra una cierta analogía con la famosa banda de Möbius.

La lógica del juego

El 25 de Junio de 1857, un joven matemático llamado Charles Lutwidge Dodgson se encontraba en su habitación del Christ Church, escuchando los ecos de un baile celebrado en el salón. En ese momento escribió un poema a modo de acróstico, cuya estrofa más conocida es la que sigue:

¿Qué me importa a mí ese jolgorio, 

si mi mente está llena de potencias y quebrados?

Es evidente que este matemático sabía divertirse. Pero que se trataba de un profesional serio tampoco puede negarse, a juzgar por los títulos de algunas de sus obras, entre los que destacan: "Fórmulas de trigonometría en el plano", "Notas sobre los dos primeros libros de Euclides", "Guía del estudiante de matemáticas" o "Tratado elemental sobre determinantes". Excitante, ¿no es cierto? Además de estas obras de carácter académico, se dedicó también a diversos aspectos de la matemática recreativa, exponiendo numerosos problemas de ingenio, así como diversos juegos y métodos mnemotécnicos para recordar fácilmente largas retaílas de fechas y cifras. Se trataba de un intelectual de la Inglaterra victoriana del S. XIX, gran aficionado a la fotografía y a los paseos en barca.

El paciente lector que no haya empezado este artículo por el final se preguntará seguramente:

"¡Bueno! ¿Y quién demonios era?"

Quizás podamos ayudarle a aclarar sus ideas citando algunas de las obras, de índole no matemática, por las que es más conocido: "La caza del Snark", "Silvia y Bruno" y, especialmente, "Alicia en el país de las Maravillas" y "A través del espejo". Hablamos, como ya os podréis figurar, de Lewis Carroll, autor que sigue fascinando a niños y adultos con su pasión por los juegos y la lógica. Resulta fascinante recorrer sus libros y descubrir en cada nueva lectura ocultas alusiones a diversos aspectos de las matemáticas. 

El hombre tímido, algo sordo y tartamudo que se dedicaba a dar clases de matemáticas a jóvenes estudiantes durante el día, se transformaba durante sus largas noches en vela en un atrevido e ingenioso cuenta-cuentos. Las inocentes historias contadas a las hermanas Liddell durante un paseo en barca se convertían en delirantes aventuras en un mundo subterráneo más allá de la lógica y lo irracional. Es justamente esta antítesis, que algunos autores llegan a calificar de "desdoblamiento de la personalidad" (lo cual yo considero quizás algo exagerado), uno de los aspectos que más han fascinado de la personalidad de Carroll/Dodgson. Y sin embargo, cuando hablamos de ella, muy pocas personas conocen la faceta seria que servía en cierto modo de "tapadera" al irreverente matemático. Al leer una biografía suya, las matemáticas y los juegos se entrelazan de tal modo que pasan a ser casi indistinguibles: podemos aprender lógica deduciendo que "ninguna golosina deliciosa es perjudicial", adivinar números imposibles, encriptar mensajes con matrices o construir con un pañuelo un recipiente que contenga el universo entero.

Me gustaría animar a los lectores que quieran aprender y disfrutar algo más con esta faceta de Lewis Carroll, tan importante para comprender su obra literaria, recomendándoles un excelente libro publicado por la editorial Turner titulado "Lewis Carroll en el país de los números". Su autor, Robin Wilson, ha llevado a cabo un exhaustivo trabajo de documentación y recopilación de datos, que incluyen numerosos artículos poco conocidos del autor, así como problemas, juegos y pasajes de sus obras; todo ello hilvanado con gran maestría y narrado con un estilo agradable y distendido, haciendo de esta biografía una obra amena incluso para aquellos lectores que no suelan tratar con matemáticas (yo diría que es amena especialmente para ellos). 

Para concluir este pequeño artículo y aportar pruebas que avalen mi tesis, me gustaría exponer dos "perlas" que me han parecido especialmente interesantes, y que suelen aparecer en la mayoría de libros dedicados a Lewis Carroll. La primera de ellas es el siguiente poema, a él atribuido:

I often wondered when I cursed, 

Often feared where I would be  -

Wondered where she´d yield her love

When I yield, so will she,

I would her will be pitied!

Cursed be love! She pitied me...

(A menudo me preguntaba, cuando renegaba

muchas veces temía por dónde andaría...

Me preguntaba cuándo llegaría a amarme,

si me rindo, también cederá ella.

¡Ojalá su voluntad fuera respetada!

¡Maldito sea el amor! Ella me compadecía...)

Quizá parezca insulso a primera vista, pero... ¿Habéis probado a leerlo palabra por palabra de arriba a abajo, por columnas, además de de izquierda a derecha, por filas? ¡Es el mismo poema!

Para finalizar, expongo brevemente el método inventado por Lewis Carroll para adivinar, dada una fecha numérica (por ejemplo 9/02/1991), el día de la semana en el que sucedió. Hay que remarcar que este método sólo funciona para fechas posteriores a la corrección del calendario gregoriano en 1582:

Método de Carroll para averiguar el día de la semana

en que cae cualquier fecha

1º.- Dividir la fecha elegida en cuatro partes, es decir, la cifra que representa los siglos, el número del año del siglo correspondiente, el mes y el día del mes. 

Ejemplo: si la fecha es 18 de Septiembre de 1783, la descomponemos en: 17  |   83   |   9  |   18  |

2º.- Calcular las cuatro operaciones siguientes, sumándolas, sea cual sea el resultado, al total de las operaciones ya calculadas. Cuando algún resultado, o el total, sea superior a 7, dividir por 7 y memorizar tan sólo el resto.

- En la cifra indicativa del siglo: dividirla por cuatro, restar de 3 el resto y multiplicar el resultado por dos.

Ejemplo: 17 dividido entre 4 nos da un resto de 1; si restamos 1 de 3, nos queda 2, que multiplicado por 2 nos da 4.

- En la cifra indicativa del año: sumar el número de docenas, el sobrante, y el número de cuatros que tenga el sobrante. 

Ejemplo: 83 es igual a 6 docenas más 11; si sumamos ambas cantidades nos da 17, más 2 (11 = 4 + 4 + 3 , hay 2 cuatros), 19, es decir (dividiendo por 7), resto 5. Total: 9, es decir, 2 (resto de dividir nuevamente por 7).

- En el mes: si comienza o finaliza por vocal en inglés, restar de 10 la posición numeral que ocupa en el año. Esta cifra, más el número de días de dicho mes, nos dará el numeral del mes siguiente. El numeral para Enero es el 0; para Febrero o Marzo (tercer mes) es el 3; para Diciembre (duodécimo mes) es el 12. 

Ejemplo: El mes de Agosto es el mes 8, de modo que si restamos 10 - 8 = 2. Por tanto el numeral de Septiembre será 2 + 31 (número de días de Agosto) = 33, es decir, 5 (resto de dividir por 7).  Sumándolo al resultado anterior nos queda 2 + 5 = 7, es decir, 0.

- En el día: es exactamente el día del mes.

Si la fecha corresponde a Enero o Febrero de un año bisiesto, habremos de rectificar la cifra así obtenida restándole 1 (añadiendo antes 7 si el total fuese 0). Hay que recordar que todos los años divisibles por 4 son bisiestos, a excepción de aquéllos que marcan el inicio de cada siglo, que no sean divisibles por 4. Por ejemplo, 1800 no es bisiesto pero 2000 sí lo es.

El resultado final nos dará el día de la semana, habida cuenta de que el domingo es el 0, el lunes es el 1, y así sucesivamente. 

Ejemplo: 18 nos da 4, que sumado al resultado anterior nos da 0 + 4 = 4. Respuesta: Jueves

Podéis creerlo o no, pero Lewis Carroll afirmaba que la cuenta mental le llevaba unos 20 segundos después de cierta práctica. Yo le rondo los 30 o 40 después de hacerlo varias veces.

¡Sed lógicos, y sed felices!

  

Contando pollos

Una pregunta aparentemente banal - ¡cómo nos gusta a los matemáticos esa palabra! - que podría ocurrírsele a uno es la siguiente: ¿cómo contarán los pollos en una tribu cuyo sistema de numeración se reduzca a 1, 2, infinitos?

Supongamos que un explorador interesado en las costumbres de los Araguamaneos del sur llegara a su tribu con la intención de que le explicaran la estructura jerárquica del poblado. Ellos le responderían que el respeto tributado a cada núcleo familiar depende del número de pollos que poseen, por ser una medida de la capacidad económica de cada familia (se trata de un sistema que pronto desembocará en el capitalismo más feroz). Hasta este punto, todo resulta más o menos aceptable - excepto para algún sector comunista, pero esto es otra historia. El problema radica en que los habitantes del poblado jamás se han visto en la situación de contar más allá del número 2; vamos, que ni se plantean qué pueda haber más allá.

Sorprendido por este hecho, nuestro explorador les pregunta cómo es posible que sepan cuál de dos familias tiene más pollos en el caso de que ambas posean más de 2 - cosa que en familias de clase media-alta ocurre en numerosas ocasiones. El chamán de la tribu, encargado de las cuestiones científicas (ahora se explica por qué no cuentan más allá de 2), le explica a nuestro atónito explorador el sistema que utilizan: cada familia coloca a sus pollos en fila india, de manera que las dos filas desfilen emparejadas por la puertecita del corral. En el momento en que los pollos de una de las dos familias se acaben, la fila correspondiente dejará de pasar por la puertecita del corral, y la otra continuará desfilando. De ese modo, la familia cuyos pollos hayan quedado desparejados será, como resulta lógico, la que más pollos tiene.

Y todo este rollo patatero, ¿por qué?

Georg Cantor (1845-1918)

La respuesta es algo más profunda de lo que podría pensarse en un principio. Hemos de remontarnos al último cuarto del S. XIX, más concretamente a 1874, año en el que aparece el primer trabajo del matemático Georg Cantor sobre teoría de conjuntos, hoy en día considerada la base de las matemáticas modernas. En su estudio de las magnitudes infinitas, que en esencia son tratadas como conjuntos infinitos, Cantor va a introducir una noción revolucionaria: los cardinales transfinitos. Este nuevo concepto sacude todos los cimientos intuitivos de nuestra experiencia cotidiana, puesto que afirma que existen infinitos "mayores" que otros.

**** Punto crítico de desbandada general; rogamos por favor 

mantengan la calma y continúen leyendo detenidamente ****

Vamos a utilizar la amena historia anterior para intentar aclarar qué significa que un infinito sea "mayor" que otro. Comenzando por el principio: llamamos cardinal de un conjunto al número de elementos que contiene dicho conjunto. Hasta aquí bien, pero claro, ¿cuál es el cardinal de los conjuntos que son infinitos, y cómo podemos compararlos, si ni siquiera podemos contarlos? Aquí entra en juego el concepto de cardinal transfinito introducido por Cantor.

De todos los conjuntos de números infinitos con los que tratamos, podemos aceptar sin mucha dificultad que el más reducido de todos es el de los números naturales, denotado por , con los que estamos habituados a tratar: 

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ..........

El cardinal transfinito de este conjunto se denomina (es decir, "aleph sub-cero"), y es el más pequeño posible. Ahora, recordando las enseñanzas del chamán de la tribu, vamos a establecer un método efectivo de comparación con otro conjunto infinito, haciendo que sus elementos desfilen emparejados en dos filas indias, exactamente igual que con los pollos (el término técnico en matemáticas para este emparejamiento se denomina correspondencia biyectiva).

¡Dicho y hecho! Tomemos un conjunto infinito distinto, el de los números enteros o , que como ya sabemos son los de la forma:

........, -3, -2, -1, 0, 1, 2, 3, .........  

Aparentemente uno podría pensar que este conjunto es evidentemente mayor que el de los números naturales, puesto que éstos están contenidos en él. Sin embargo, y contra toda intuición, vamos a "emparejar" ambos conjuntos y veremos que "ningún pollo queda descolgado":

Asociemos al número 0 (de los números enteros) el número 1 (de los números naturales). Al número 1 (de los números enteros) le corresponderá el número 2 (de los números naturales); al número -1 (de los números enteros) le corresponderá el número 3 (de los naturales), y así sucesivamente, como muestra la imagen siguiente:

Observamos que, por muchos pollos que hagamos desfilar por la puertecita del corral, todos seguirán emparejados, sin que ninguno de ellos pueda quedar descolgado. Acabamos de demostrar que ambos conjuntos tienen el mismo cardinal transfinito, que es, como ya hemos visto, .

En este momento surgen algunas cuestiones, que resolveremos en un futuro artículo (si vemos que éste ha tenido aceptación):

- ¿Qué ocurre con los demás conjuntos de números: los racionales, los reales...?

- ¿Qué conjuntos infinitos son "más grandes" que el de los números naturales?

- ¿Hay más números pares positivos que números naturales? 

- ¿Cómo es que un chamán de una tribu se maneja mejor con conjuntos infinitos que algunos catedráticos de matemáticas alemanes del S. XIX, a juzgar por la mala aceptación de las teorías de Cantor?

¡Hasta el infinito, y más allá!

El hombre

 I.Veni

Cuando recobró el conocimiento, se encontró tendido boca arriba en la oscuridad más absoluta. Debía de haber estado aletargado durante mucho tiempo, pero a pesar de ello sus ojos no parecían haberse acostumbrado a la falta de luz, y por más que se esforzara no podía llegar a atisbar los límites de la habitación donde se encontraba. Estiró sus extremidades en todas direcciones, más para cerciorarse de las dimensiones de su celda que para desentumecerse, y se tranquilizó al comprobar que, al menos, no estaba encajonado del todo. Entornando los ojos, miró a su alrededor intentando captar alguna señal de luz que le permitiera distinguir puertas o ventanas, pero todo estaba sumido en la negrura.

“¿Cómo he llegado hasta este lugar?”, se preguntó incorporándose asustado, “¿Quién me ha encerrado aquí y por qué?”. Sentado en cuclillas con las palmas de las manos apoyadas sobre el suelo, pudo sentir que se trataba de una superficie lisa y fría, como de mármol pulido. Esto le reconfortó, sin que él mismo supiera por qué. De alguna manera, parecía como si todos los recuerdos que había tenido en su vida relacionados con ese tacto agradable le condujeran inconscientemente a algo positivo, aunque él no pudiera acordarse con precisión de ninguna situación en particular. No obstante, esas sensaciones no eran del todo satisfactorias, pues no daban explicación alguna de su situación ni de lo que iba a sucederle. “A fin de cuentas”, reflexionó mientras deslizaba la mano por el suelo, “no es costumbre fabricar mazmorras de mármol pulido”.

Se levantó lentamente, temeroso de comprobar la altura real a la que se encontraba el techo de su habitación, pues todo lo andado hasta ese momento podía desvanecerse en caso de que éste no fuera lo suficientemente alto como para poder ponerse de pie. Con un inexplicable sentimiento de gratitud, comprobó que no sólo podía erguirse completamente sin dificultades, sino que también era capaz de estirar completamente sus brazos hacia arriba sin encontrar oposición. Satisfecho, miró desafiante a su alrededor, como intentando sorprender a las paredes que sin duda alguna le rodeaban antes de que éstas le descubrieran a él. Sin embargo, por más que observara, la habitación sólo le transmitía una sensación de infinitud muy desagradable y opresiva. Al no encontrar ningún rincón que le sirviera de refugio, el instinto le hizo permanecer inmóvil donde se encontraba, con esa sensación de vértigo que produce no conocer los límites de una estancia oscura. Poco a poco fue bajando hasta volver a la situación anterior, colocándose en cuclillas, esta vez con los brazos rodeando sus piernas para intentar protegerse de ese espacio tan horriblemente inmenso e inabarcable. Todo lo que sentía era un indignante contraste entre cercanía y lejanía, fruto del desconocimiento y la inseguridad. Aquella cárcel no era una cárcel normal, ni siquiera de mármol. Aquella cárcel era de aire.

 Tras unos minutos que a él le parecieron horas, comenzó a reflexionar sobre las causas y las consecuencias de su reclusión, así como sobre las posibles dimensiones de la habitación donde se hallaba. No conocer dónde se encontraba le agobiaba a cada instante, pero la imposibilidad de apoyarse en una pared le resultaba aún más insoportable. El riesgo de que alguien hubiera colocado algún tipo de trampa a su alrededor aprovechando la oscuridad que le envolvía le impedía moverse, y poco a poco fue sintiéndose más y más nervioso, con esa sensación de vacío en el estómago que experimentamos cuando no sabemos a qué nos enfrentamos. La exploración de su entorno inmediato le había proporcionado seguridad en sus actos mientras la había llevado a cabo, pero la inactividad a la que se había visto obligado inmediatamente después le había hecho sentir de nuevo y con más claridad su propia impotencia, lo absoluto de su ignorancia.

Observando con inquietud lo impenetrable, se dio cuenta de que ni siquiera podía distinguir sus propias manos en la oscuridad. Parecía como si todo a su alrededor quisiera asfixiarle lentamente, invadiendo su cuerpo, cerrando muros en torno a él como una niebla de acero implacable. En ese momento, una terrible expresión de terror desfiguró su cara y sus miembros y todo su cuerpo comenzaron a agitarse de manera incontrolable. Gimiendo y suspirando, se tapó la cara con las manos temblorosas. Había tomado conciencia de su propia soledad. 

II. Vidi

Al volver en sí, se encontró de nuevo tumbado en el frío mármol, completamente quieto. No soplaba viento, y la atmósfera era fría y seca, como la de una cripta. Sentándose de nuevo, esta vez con las piernas cruzadas, abrió los ojos y miró hacia arriba. ¡Cuál sería su sorpresa cuando vio un pequeño punto luminoso justo encima de su cabeza! Levantándose de un salto, se frotó los ojos para asegurarse de que había visto bien. “¿Cómo es posible que no me haya percatado antes? Estoy seguro de que hace un momento no había ninguna luz allí arriba”. Envalentonado por su descubrimiento, comenzó a tantear a su alrededor con pies y manos para cerciorarse de que no había desniveles ni agujeros, y así avanzó unos metros. De repente observó otros tantos puntitos luminosos alrededor del primero, que hacían la oscuridad reinante algo más soportable. Mirando continuamente en dirección a las lucecitas, avanzó un par de metros más y comprobó que, a medida que caminaba, iban apareciendo más puntos de luz en una bóveda aparentemente muy lejana.

Caminando con cuidado y tanteando continuamente, comenzó a darse cuenta de que no había palacio alguno cuyo salón de fiestas fuera comparable en extensión a aquella sala, y concluyó que debía estar al aire libre o dentro de un recinto inmenso, a la merced de algún retorcido bromista que había querido gastarle una broma muy pesada. Los puntos de luz, cuyo número era ya considerable, comenzaban a aportar algo de claridad al lugar, aunque éste era todavía inabarcable por los sentidos. “No puedo entender dónde me he metido, ni qué crimen he debido cometer para llegar a esta situación, y como siga andando sin rumbo acabaré perdiéndome, pero; ¿Qué puede importar eso, si ni siquiera sé dónde están los límites de este lugar?”

Miró nuevamente a su alrededor, y observó sorprendido que los puntos que guiaban su camino en la oscuridad formaban un patrón claro, como una amplia curva luminosa que iba encendiéndose sin cesar. Uno tras otro aparecían nuevos destellos repentinos, y en un momento dado, para su asombro, observó que la curva descrita era cerrada. “Podría ser una elipse, o incluso una circunferencia, por la forma que parece tener. Quizás se trate del límite de esta gigantesca habitación”.

¿Lo sería realmente? Un rápido vistazo le hizo detenerse en una silueta, parcialmente iluminada, situada en lo que parecía ser el centro de la sala. “¡Al fin, un punto desde el que puedo orientarme!”, pensó. Sin tenerlas todas consigo, avanzó pesadamente en la penumbra, acercándose lentamente hacia el objeto, que cada vez se hacía más y más grande. No cesaba de tantear el suelo sobre el que pisaba, para estar seguro de que no hubiera algún desnivel o - ¿quién sabe? – Quizás un pozo sin fondo.

El objeto que acaparaba su atención era, como él vio claramente, una gigantesca columna de aspecto amenazador y asombroso diámetro. Hacia la mitad de su altura se podían observar dos pronunciados resaltes, uno más ancho que el otro, así como un tercero en lo que parecía ser su parte superior. Aquel portentoso monumento le recordó a un tótem gigantesco, pero era imposible que una fuerza humana pudiera haber levantado sobre la tierra una figura así, construida al parecer de una sola pieza. Aquello debía de haber yacido sobre esa llanura desde el principio de la creación, sin ninguna duda. El color de aquel titán parecía gris, y sorprendentemente, descubrió que su tacto era parecido al del metal. La solemnidad de semejante coloso era indescriptible, y él tuvo la certeza de que, definitivamente, no se encontraba en ninguna mazmorra. El silencio sepulcral que le rodeaba seguía siendo total, o al menos ésa era la sensación que tenía, arrebatado en su contemplación del titán que tenía enfrente.

De repente, un zumbido monótono apartó sus pensamientos de la columna. “¿Acaso se está abriendo una puerta? Por la magnitud del ruido, deberían ser inmensas.” Tras acostumbrarse al nuevo sonido, cuyo ritmo juzgaba al principio informe, distinguió claramente una pauta regular y espaciada, que le pareció similar al de los golpes dados por el capataz en una galera. El eco era furioso, como el de un gigantesco látigo restallando, y la uniformidad de los golpes era tan grande que sobrecogía. “No puede haber nadie capaz de parar algo así, ese sonido es indudablemente el del destino”. Comenzó a pensar en la posibilidad de que estuviera muerto, pero desechó rápidamente semejantes pensamientos. Aquello no era un sueño, no podía serlo.

III. Vici 

Absorto como estaba en el sonido que no parecía tener fin – ¿acaso  habría tenido un comienzo? – no se dio cuenta de que una enorme silueta, surcando el aire, se iba acercando a él, muy por encima del lugar donde se hallaba. Aterrado, miró hacia arriba en el último momento, cuando la gigantesca sombra ya se encontraba sobre él. Se cubrió la cabeza con las manos, arrojándose al suelo, y en esa posición permaneció hasta percatarse de que nada había pasado. Alzando de nuevo la vista, vio que la sombra, un aspa gigantesca que apuntaba a las lucecitas, se alejaba de él a grandes sacudidas, acompañado por los retumbantes golpes. Sencillamente, no podía creerlo, pero el que pudiera o no le era completamente indiferente a la poderosa silueta, la cual finalmente rodeó la columna y volvió a su posición inicial, sin detenerse. Mirando de nuevo al gigantesco tótem, observó que el aspa estaba conectada a la parte superior, donde se encontraba el ensanchamiento que había observado antes.

Sudoroso y temiendo lo peor, rodeó corriendo la columna. Jadeando, los tremendos golpes ¡bum… bum… bum! Le parecían irse deteniendo progresivamente, pero eso tan sólo era una sensación provocada por su estado de ansiedad. Cada zancada que daba le dolía como una puñalada en el corazón, y no podía dejar de correr al ritmo de los golpes ¡bum… bum… bum!. Los pensamientos se agolpaban en su cabeza, cruzándose desordenados. No podía suceder lo que él temía, porque era absurdo, y porque sencillamente no podía ser, o al menos eso pensaba él, pero, ¿pensaba…? – ¿O tan sólo corría? Las respuestas le llegaban a la mente, y él tan sólo añoraba el momento en que únicamente había habido preguntas. Se detuvo, el rostro desencajado, y se cayó de rodillas con las manos cubriendo su rostro. Gritaba y lloraba, y sus lágrimas se mezclaban con el sudor.

En ese momento amaneció. Y al siguiente instante, se hizo mediodía

Deslumbrado por la cegadora luz que le envolvía, no pudo soportarla y tras intentar mirar arriba, volvió a cubrirse la cara con las manos. Un gigantesco rostro, mayor que todo lo que él podía haber imaginado, le miraba con benevolencia – o eso le pareció a él – cuando por fin pudo alzar la vista. Era la personificación de todo lo que él creía que era bueno, eterno y hermoso. Bajando la cabeza, observó dos aspas por debajo de la que había visto antes. La primera era un poco más corta que la que se movía, y la tercera, aparentemente inmóvil, era la más pequeña de las tres. Todas tenían su origen en los resaltes de la poderosa columna central, gris metalizado. Cada resalte era el principio - ¿o el final? – de cada aspa. El ritmo, invariable, le resultaba familiar. El lugar donde se encontraba se trataba, sin ninguna duda, de una enorme estancia circular con el suelo de marfil sobre el que, al pie de las paredes, aparecían trazados en orden los números del 1 al 12. Entre el gigantesco rostro y él había una cubierta acristalada, plana, de bastante grosor, que abarcaba toda la superficie.

Los golpes continuaban, rítmicos, sin cesar, a medida que la enorme aguja - la más larga de todas - continuaba su carrera circular. A cada golpe, ésta daba un paso.

“¿Estoy en el cielo, Dios mío? ¡Por favor, respóndeme!”, gritó, con una voz más potente que los golpes rítmicos. ¡tic..., tac..., tic..., tac...! A los cuatro segundos, uno por cada golpe, se oyó con una voz maravillosa, ensordecedora, pero más armónica de lo que él podría haber imaginado jamás - o al menos eso le pareció a él:

- ¡Pero qué tarde es, las tres y veinte! Y mi mujer esperándome en casa…

El bello transeúnte se guardó el reloj de cuerda en el bolsillo, y con raudo paso se encaminó, el maletín bajo el brazo, hacia su casa.

Pequeño inciso informativo

¡Bueno! Después de inaugurar el blog y de haberme estrenado al fin, uno ya se siente un poco más seguro acerca de qué hacer con esta herramienta y, si bien sigue sin haber un objetivo claro, al menos hemos echado a andar hacia alguna dirección - lo cual no es poco decir. 

El motivo de esta pequeña entrada es simplemente informar a los lectores que se hayan preguntado el motivo de citar tan extensamente a Schiller en la columna de la derecha de mi intención de exponer una reseña de los autores que vaya leyendo este verano a intervalos de tiempo regulares (aproximadamente 10 días o una quincena). Espero tener tiempo de poder hacer una pequeña entrada para exponer las reflexiones que surjan acerca del libro leído, evitando como es lógico todo spoiler que pueda frustrar a futuros lectores del autor reseñado. Nunca olvidaré mi decepción cuando leí la introducción a "Las desventuras del joven Werther" en la edición de Cátedra, en la que se exponía clarísimamente, como si fuera un hecho de cultura popular, el final del libro. Queridos lectores, jamás leáis una introducción de un libro famoso (en especial los de Cátedra) antes de leer la historia. Para profundizar en lo leído, tiempo habrá.

Saludos.

Ein musikalisches Opfer (A musical offering)

En "Gödel, Escher, Bach", la obra más conocida de Douglas R. Hofstadter, el autor muestra en un pasaje especialmente afortunado el paralelismo existente entre una pieza de música clásica y una demostración matemática. En concreto, el puente que relaciona unos elementos con otros es, en palabras del autor, "el sentido matemático de la tensión, íntimamente relacionado con su sentido de la belleza". 

Johann Sebastian Bach (1685-1750)

Esta tensión se puede sentir, al escuchar una pieza musical, en las progresiones armónicas que nos permiten saber cuál es la tonalidad de la obra, sin llegar a resolverla. En el caso de la demostración matemática, la tensión es provocada al adentrarse en la lectura de los razonamientos, los cuales se alejan cada vez más de los postulados iniciales, sin que veamos exactamente cuál será, finalmente, la "resolución". Así mismo, tenemos también momentos de "respiro" tanto en la obra musical como en la demostración: en una pieza de tipo AABB se "arriba a una resolución momentánea, aun cuando no se haga en la nota tónica". En el ámbito matemático, haríamos referencia a los resultados intermedios conocidos como "lemas" - pruebas de menor profundidad que son utilizados en el cuerpo principal de la demostración.

En uno y otro caso, la sensación que tiene el oyente/lector es la de alguien que emprende un viaje por un camino, dejándose llevar, sin saber hacia dónde se dirige. En la pieza musical, el punto de partida es la nota tónica, mientras que en la demostración se trata de las hipótesis iniciales. A medida que la pieza avanza, el oyente avezado puede intuir con mayor o menor dificultad hacia dónde se encaminan los pasos, y de qué forma va a concluir el viaje. El matemático que lee una demostración no necesita ninguna información añadida, puesto que el final de la prueba debe ser exactamente el enunciado que se pretende demostrar.
 

En ambas creaciones existe un momento en el cual se tiene la sensación de que nos encaminamos indudablemente hacia la conclusión. En casi todas las demostraciones - o al menos, diría Hardy, en las "elegantes" - existe una idea fundamental alrededor de la cual se estructura toda la prueba y, al llegar a ese paso crucial (la llamada muchas veces "idea feliz") , el matemático siente un profundo escalofrío de admiración y de complacencia estética. Es en ese instante cuando vemos la luz al final del túnel y, al igual que ocurre en el desenlace de la tensión musical, nos lanzamos ávidamente a disfrutar de cada uno de los pasos siguientes,  sabiendo que toda la obra está ya en nuestras manos. 

 En mi opinión, no existe una obra mejor que la de Johann Sebastian Bach para exponer con claridad este paralelismo tan íntimo. A veces se suele objetar que, si uno quiere buscar la apariencia matemática en un tema musical, lo mejor es remitirse a los compositores del clasicismo o, incluso, a los de la segunda escuela vienesa, quizás por su sobriedad o por su estricta adhesión a unas normas formales. Sin embargo la obra del organista de Leipzig aporta, a diferencia de las arriba mencionadas, una clara e importante "distinción entre figura y fondo" ya remarcada por Hofstadter en su libro. En este caso nos referimos a la relación de tensión existente entre la línea melódica principal y el acompañamiento, que Bach supo aprovechar con total maestría para desarrollar su potente visión musical. Una de las pruebas más elocuentes en este sentido es su inmortal Canon 5 a 2 Per Tonos "Ascendenteque Modulatione Ascendat Gloria Regis" (Así ascienda la gloria del rey como ascienden las modulaciones). En suma, la tesis que mantenemos es que la profusión y diversidad de líneas melódicas aparentemente independientes entre sí, pero entrelazadas con maestría para crear los efectos más sorprendentes, es esencialmente la que otorga a la obra de Bach esa profundidad de la que adolecen otros compositores posteriores, más sobrios en ese sentido. Es justamente en la extraordinaria capacidad del autor por aunar temas en apariencia tan dispares donde se manifiesta con toda claridad la profundidad estética de su proceso de creación, que se nutre evidentemente de lo formal para ir siempre un poco más allá. Eso es, a mi juicio, lo extraordinario del genio de Bach. 

Por esta razón creo que Bach es el más matemático de los compositores. Porque las matemáticas, al igual que sus composiciones, se nutren de lo formal para ir, siempre, un poco más allá...

Aquí tenéis esta pequeña ofrenda musical. Para una descripción muy bella y completa de este maravilloso canon, remito nuevamente al libro de Douglas R. Hofstadter "Gödel, Escher, Bach: un Eterno y Grácil Bucle" pág. 12 (Ed. Tusquets 2009).

Inauguración solemne

El vértigo de la hoja en blanco es tanto más intenso cuanto mayor es la inseguridad respecto a nuestras capacidades. Y el primer escrito a publicar es indiscutiblemente una hoja en blanco de las peores características. Me perdonaréis que, en esta caída por la madriguera del conejo blanco - así es como me siento al iniciar esta prometedora aventura - intente aferrarme a algún saliente en la pared, o a alguna raíz que sobresalga. Este pequeño texto fue escrito hará un par de años, y puede servirme como punto de apoyo, si no para mover el mundo, sí al menos para dar los primeros pasos por el blog sin caerme.

La idea que subyace es la de escribir "a la manera de...", práctica que según parece, Marcel Proust llevaba a cabo como ejercicio literario, intentando imitar algo del estilo de otros escritores que a él le parecían interesantes. En este caso, soy yo quien intenta trasladar algo de su prosa, con mayor o menor fortuna.

 Divertimento Proustiano

A menudo recuerdo las tardes otoñales en las que salía a dar un paseo solitario por el parque de la Taconera. Durante toda la semana esperaba con inquietud que llegara el anhelado viernes, el cual, como antesala de un fin de semana apacible y sosegado, me brindaba la posibilidad de dedicar largas horas de la tarde a la contemplación, la meditación, y a ese placer tan grato que nos proporciona tomar decisiones tan sencillas e inocentes como “girar a la derecha por una bocacalle”, o por el contrario “seguir recto a la sombra de los árboles”, en contraposición a la gravedad y la trascendencia de las decisiones que muchas veces nos vemos obligados a tomar en nuestra vida cotidiana. Solía llevar a esos paseos algún libro conmigo, en parte por si la meditación se tornaba apatía, pero ante todo por emular a los caballeros ingleses de la época victoriana, en cuya opinión había tan sólo dos cosas que un verdadero gentleman podía llevar consigo por la calle: un libro, o un melón (típica muestra del humor británico). Uno de mis acompañantes más asiduos era aquel “Tractatus Logico-Philosophicus”, del filósofo Ludwig Wittgenstein, en cuya comprensión residían en aquel momento mis esperanzas de hallar una explicación consistente de los problemas de la humanidad. Sin embargo, pocas veces lo leía al aire libre; más bien esperaba a llegar a la invariable meta de mi paseo, la tetería, para pasar algunas horas ojeándolo mientras tomaba un té restablecedor.

Al adentrarme en el parque era como si un mundo nuevo se abriera ante mí; como si de alguna manera hubiese accedido a una puerta en el tiempo que me llevara a otro mundo. Era un sentimiento de egoísmo inocente muy placentero el que yo me imaginara, como único caminante, que el parque entero me pertenecía, y cuando me topaba con otro transeúnte no podía dejar de pensar que era él quien estaba invitado a mi fiesta en el jardín, que yo había traído el Sol y los pinos y les había ordenado que tomasen forma para el disfrute de cuantos por allí paseaban. Así es, en cierto modo, la adolescencia. El silencio y la paz del vetusto parque hacían fijarse mi atención en detalles a los que normalmente no otorgamos importancia, como la disposición de las ramas en los árboles, el tipo de semillas de cada uno de ellos, las distintas tonalidades de sus hojas o la rugosidad de sus troncos. También me era perceptible el canto de los pájaros y el lejano murmullo de una fuente juguetona, la cual, escondida entre setos y arbustos, dominaba el centro de un pequeño estanque circundado por salvias espigadas de un rojo vivo y enérgico, atrayéndome hacia sí con sus trinos y su transparente salpicar. Allí se encontraba el corazón del parque, el altar sagrado de aquel templo vegetal, baluarte inexpugnable que, orgulloso, se alzaba frente al devenir del tiempo sin importarle los evidentes signos del desgaste que, fruto del descuido y la desidia, se hacían notar por todo el jardín.

El paseo que conducía a aquella fuentecita se hallaba franqueado por pares de columnas desnudas y enlazadas, las cuales, indiferentes ante lo que pasara fuera del recinto que delimitaban, protegían al caminante del resto del mundo. Las ramas bajas de los pinos que las rodeaban las acariciaban suavemente, llegando a veces cerca del suelo. ¡Qué deleite el ser por un momento el sumo sacerdote de aquel santuario! Podía sentir el movimiento de cada rama, de cada brizna de hierba; era capaz de respirar al mismo tiempo que lo hacían aquellos colosos que, sin dejar de apoyar su planta en la tierra, aspiraban a tocar el cielo con sus copas, orgullosos, contemplándome desde las alturas. Y yo me sentía dichoso de poder  observar aquel espectáculo multicolor y silencioso que estaba mostrándose ante mí, sintiendo la calma de las hojas rítmicamente mecidas por la brisa otoñal.

Entre tanto me volví para descender por las escaleritas que llevaban de nuevo a la calle principal del jardín, y me fijé en las farolas que, esperando a alumbrarse en su turno de guardia, dormitaban frías y silenciosas, como extrañas en un mundo que no les pertenecía y que en vano ellas se esforzaban en dominar, superadas siempre por la incuestionable majestad de los nobles troncos y de las interminables ramas que se desplegaban a su alrededor. “Podemos rodear vuestra luz hasta hacerla desaparecer, tened cuidado”, parecían decirles, amenazadoras. Pero las farolas no se inmutaban, sino que se limitaban a hacer su trabajo sin rechistar, charlando de vez en cuando con un pájaro que ocasionalmente, se posara sobre su corona. Jugando a esconderme del sol por las sombras y los claros que se abrían alrededor mía, atravesaba lentamente los senderos entre los parterres inundados de flores multicolores, las cuales, por su disposición calculada y artificial, contrastaban con los matojos salvajes que se abrían paso desesperadamente en los lugares más insospechados. El otoño, ya avanzado, había arrastrado consigo multitud de hojas que, todavía algo verdes y húmedas por las últimas lluvias, se extendían por todo el jardín formando una alfombra vegetal que sepultaba a veces los caminitos transitables, por lo que me veía obligado a apartarlas a medida que iba avanzando. Feliz por la hazaña de civilizar la naturaleza desordenada, me entretenía en abrir caminos por entre los pequeños setos y los arbustos, dando vueltas, a veces en círculos, animado por los espontáneos cantos de los pájaros que, descansando en las ramas semidesnudas, observaban mi obra deleitados, o al menos eso me parecía.

¡Cuán distinta parecíame aquella naturaleza en las oscuras tardes de diciembre, cuando los tonos verdes se transformaban en gamas de gris y, antes de que pudiera uno percatarse, se sumía el parque en la oscuridad más absoluta! Recuerdo alguna visita esporádica al recogido café vienés, aquel faro para los paseantes que servía de refugio contra la inclemencia del tiempo y la oscura soledad que reinaba entonces en la Taconera. Desde mi asiento podía entrever, confundida con los innumerables reflejos de las farolas que se estrellaban contra los cristales de las ventanas, aquella fuente mágica, inigualable contraste entre la inmovilidad de las esencias que formaban su cáliz y el devenir que mostraba el borboteo incesante del agua que emanaba. No había vistas mejores del templo que aquellas y, en perspectiva, podía yo imaginarme aquella disposición de los árboles, los setos y los caminos como una verdadera catedral de la naturaleza en cuyo crucero se encontraba la fuentecita, rodeada por un banco de ladrillos que hacía las veces de girola para los peregrinos quienes, atraídos por la santidad del lugar, quisieran admirar las reliquias contenidas en las flores, las hojas y las ramas de aquellos gigantes rugosos que formaban las columnas del santuario. Muchas veces me preguntaba yo qué catedral podía haber más perfecta que aquella, que tenía por suelo la tierra, las ramas por arquivoltas, por capiteles las flores, y el cielo estrellado por cúpula. ¡Qué deleite aquel altar que no pedía sacrificios, sino que otorgaba toda la paz y la armonía que uno podía desear! ¡Qué tapices de hojas dentadas, lobadas, cordadas y lobuladas se fundían con el barro otoñal de las lluvias, volviéndose tierra sin que nuestros sentidos pudieran percibirlo! ¡Qué arces marcescentes de exóticos nombres, venerables semidioses, mantenían sus frutos en el aire mucho tiempo después de haberse secado las flores que les vieron nacer!

Bondadosos, los pinos observaban a los jóvenes exaltados que, no profanando el templo, sino honrándolo, corrían de un lado a otro gritándose y persiguiéndose sin cesar. Yo no podía por menos de admirar la vitalidad de la juventud que, indiferente ante la época del año, se siente renacer con cada instante vivido, haciendo rejuvenecer constantemente a quienes pueden todavía comprenderles, y propiciando el envejecimiento de aquellos que ya no comparten sus mismas emociones, habiéndolas sustituido por otras, tornándose incapaces de ver en la juventud los mismos principios que les guiaron en su infancia inocente y olvidada. No es el tiempo el que hace envejecer, sino el olvido y la incomprensión.