Contando pollos (III parte)

Tras una breve espera reanudamos nuestra serie de artículos sobre conjuntos infinitos, dispuestos a dar respuesta a las preguntas que faltan. En la anterior entrada prometimos dar una prueba de que el orden de infinitud de los números reales es efectivamente mayor que el de los números naturales - si recordáis las anteriores explicaciones, probar esto implicaría probar también que el orden de infinitud de los reales es mayor que el de los enteros y los racionales, puesto que el cardinal transfinito de todos estos conjuntos es, como ya vimos, el mismo (). 

Vamos a dar unas pequeñas explicaciones preliminares, para pasar luego a abordar el problema con mayor seguridad. El conjunto de los números reales es, expresado de una manera sencilla, el formado por el conjunto de los números racionales (fracciones) y el conjunto de los números irracionales. Éstos últimos se caracterizan por tener infinitas cifras decimales que van sucediéndose de manera no periódica; los ejemplos más famosos son, como quizá conozcáis, el número π ("pi"), el número e ("e") o el número Φ ("número áureo"). La característica que diferencia a los números irracionales de los racionales es que no podemos dar una pauta que nos permita conocer la sucesión de sus cifras decimales, cosa que sí ocurre con los segundos.

¿Cuál es la esencia de la prueba?

Möbius band, M.C. Escher

 Vamos a llevar hasta el extremo nuestra analogía de las filas de pollos. Si lo que pretendemos es mostrar que un conjunto tiene un orden de infinitud mayor que otro, lo que en realidad pretendemos es ver que al emparejar los pollos de cada familia y hacerles desfilar por la puertecita del corral, al menos uno va a quedar descolgado y perdido. Por lo tanto y en buena lógica, lo que vamos a hacer es suponer que todos están ya emparejados, para luego ver que esto es imposible. Vamos a ello:

Supongamos que tenemos una lista numerada con todos los números reales. Esto equivale a emparejar cada número natural con un número real (el orden de aparición nos da igual). Para simplificar la prueba, vamos a suponer que la lista numerada contiene los números reales del 0 al 1 (es fácil probar que el orden de infinitud de este intervalo es equivalente al de toda la recta real, cosa que no demostraremos).

Así pues, una posible lista sería la que sigue:

1. 0.132245677538323..........................
2. 0.573839728947238..........................
3. 0.683447384579397..........................
4. 0.093993828273833.........................

etcétera. Ahora vamos a fijar nuestra atención en la cifra decimal correspondiente a la posición de cada número en la lista. Por ejemplo, nos fijaremos en la primera cifra decimal del número real que ocupa la posición 1, en la segunda cifra decimal del número real que ocupa la posición 2, y así sucesivamente. Vamos a construir en base a ello un número real tan rematadamente enrevesado que será imposible que esté en la lista.

**** Rogamos a los lectores mantengan la serenidad y lean con calma;

 ni el número es tan enrevesado, ni el autor pretende un holocausto cerebral **** 

La pequeña regla que vamos a utilizar será la siguiente: para conocer la cifra decimal que ocupa el lugar p de nuestro número, observaremos el número que ocupa el lugar p en nuestra lista y nos fijaremos en su p-ésima cifra decimal. Sea n el valor de esta cifra, entonces la cifra de nuestro número será, precisamente, n+1 (en el caso de que el valor de n sea 9 , la cifra de nuestro número será 0).

Vamos a clarificar esta regla con un ejemplo en base a nuestra querida lista: ¿cuál será la primera cifra decimal de nuestro número enrevesado? Viendo la primera cifra decimal del primer número de la lista, esto es, 1, tenemos que la primera cifra de nuestro número enrevesado será 1 + 1 = 2. Sencillo, ¿no?

número enrevesado = x = 0.2.................................

¿cuál será la segunda cifra decimal de nuestro número enrevesado? Viendo la segunda cifra decimal del segundo número de la lista, es decir, 7, tenemos que la segunda cifra de nuestro número enrevesado será 7 + 1 = 8.

número enrevesado = x = 0.28.............................

Y así sucesivamente, quedando x = 0.2840..............................

Ahora viene el golpe de gracia: ¿puede nuestra lista contener al número x?  Preguntémonos lo siguiente, que es lo mismo; ¿puede nuestro número x encontrarse en un lugar de nuestra lista? o bien, dicho de otra manera, ¿puede estar nuestro número x en el lugar m de la lista, donde m es cualquier número natural?

Es claro que esto no puede ocurrir ya que, tal y como lo hemos construido, nuestro número difiere del que ocupa el lugar m precisamente en la m-ésima cifra decimal. Para verlo más concretamente: nuestro número no puede estar en el lugar "1" de la lista, puesto que, como ya observamos, la 1ª cifra del número x y la 1ª cifra del número 1 de la lista ya son distintas. Vemos con claridad que lo mismo le sucede con el 2º número de la lista, con el 3º, el 4º, y así con todos los que quiera haber.

Nuestro número x es el pollo que queda descolgado, y por tanto hemos visto que el conjunto de los números reales es necesariamente de orden mayor que el conjunto de los números naturales. Más concretamente, el orden de infinitud de los números reales es 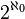, ya podéis ver que este corral entra dentro de la categoría de lo "bestia".

Los matemáticos tienen fama de parcos en palabras, principalmente porque la mayoría de ellos piensa que no es necesario añadir más cuando ya se ha demostrado algo. En este caso el artículo se ha alargado más de lo que yo pensaba, y creo que por deferencia hacia el paciente lector, vamos a acabar sin mayor esfuerzo adicional. Queda en el aire la respuesta a la pregunta ¿hay más números pares positivos que naturales? Sirva como aliciente para aquellos que se interesen por los emparejamientos de pollos. Os dejo con un recuerdo del infinito...