Una pregunta aparentemente banal - ¡cómo nos gusta a los matemáticos esa palabra! - que podría ocurrírsele a uno es la siguiente: ¿cómo contarán los pollos en una tribu cuyo sistema de numeración se reduzca a 1, 2, infinitos?
Supongamos que un explorador interesado en las costumbres de los Araguamaneos del sur llegara a su tribu con la intención de que le explicaran la estructura jerárquica del poblado. Ellos le responderían que el respeto tributado a cada núcleo familiar depende del número de pollos que poseen, por ser una medida de la capacidad económica de cada familia (se trata de un sistema que pronto desembocará en el capitalismo más feroz). Hasta este punto, todo resulta más o menos aceptable - excepto para algún sector comunista, pero esto es otra historia. El problema radica en que los habitantes del poblado jamás se han visto en la situación de contar más allá del número 2; vamos, que ni se plantean qué pueda haber más allá.
Sorprendido por este hecho, nuestro explorador les pregunta cómo es posible que sepan cuál de dos familias tiene más pollos en el caso de que ambas posean más de 2 - cosa que en familias de clase media-alta ocurre en numerosas ocasiones. El chamán de la tribu, encargado de las cuestiones científicas (ahora se explica por qué no cuentan más allá de 2), le explica a nuestro atónito explorador el sistema que utilizan: cada familia coloca a sus pollos en fila india, de manera que las dos filas desfilen emparejadas por la puertecita del corral. En el momento en que los pollos de una de las dos familias se acaben, la fila correspondiente dejará de pasar por la puertecita del corral, y la otra continuará desfilando. De ese modo, la familia cuyos pollos hayan quedado desparejados será, como resulta lógico, la que más pollos tiene.
Y todo este rollo patatero, ¿por qué?
 |
| Georg Cantor (1845-1918) |
La respuesta es algo más profunda de lo que podría pensarse en un principio. Hemos de remontarnos al último cuarto del S. XIX, más concretamente a 1874, año en el que aparece el primer trabajo del matemático Georg Cantor sobre teoría de conjuntos, hoy en día considerada la base de las matemáticas modernas. En su estudio de las magnitudes infinitas, que en esencia son tratadas como conjuntos infinitos, Cantor va a introducir una noción revolucionaria: los cardinales transfinitos. Este nuevo concepto sacude todos los cimientos intuitivos de nuestra experiencia cotidiana, puesto que afirma que existen infinitos "mayores" que otros.
**** Punto crítico de desbandada general; rogamos por favor
mantengan la calma y continúen leyendo detenidamente ****
Vamos a utilizar la amena historia anterior para intentar aclarar qué significa que un infinito sea "mayor" que otro. Comenzando por el principio: llamamos cardinal de un conjunto al número de elementos que contiene dicho conjunto. Hasta aquí bien, pero claro, ¿cuál es el cardinal de los conjuntos que son infinitos, y cómo podemos compararlos, si ni siquiera podemos contarlos? Aquí entra en juego el concepto de cardinal transfinito introducido por Cantor.
De todos los conjuntos de números infinitos con los que tratamos, podemos aceptar sin mucha dificultad que el más reducido de todos es el de los números naturales, denotado por  , con los que estamos habituados a tratar:
, con los que estamos habituados a tratar:
 , con los que estamos habituados a tratar:
, con los que estamos habituados a tratar: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ..........
El cardinal transfinito de este conjunto se denomina  (es decir, "aleph sub-cero"), y es el más pequeño posible. Ahora, recordando las enseñanzas del chamán de la tribu, vamos a establecer un método efectivo de comparación con otro conjunto infinito, haciendo que sus elementos desfilen emparejados en dos filas indias, exactamente igual que con los pollos (el término técnico en matemáticas para este emparejamiento se denomina correspondencia biyectiva).
(es decir, "aleph sub-cero"), y es el más pequeño posible. Ahora, recordando las enseñanzas del chamán de la tribu, vamos a establecer un método efectivo de comparación con otro conjunto infinito, haciendo que sus elementos desfilen emparejados en dos filas indias, exactamente igual que con los pollos (el término técnico en matemáticas para este emparejamiento se denomina correspondencia biyectiva).
 (es decir, "aleph sub-cero"), y es el más pequeño posible. Ahora, recordando las enseñanzas del chamán de la tribu, vamos a establecer un método efectivo de comparación con otro conjunto infinito, haciendo que sus elementos desfilen emparejados en dos filas indias, exactamente igual que con los pollos (el término técnico en matemáticas para este emparejamiento se denomina correspondencia biyectiva).
(es decir, "aleph sub-cero"), y es el más pequeño posible. Ahora, recordando las enseñanzas del chamán de la tribu, vamos a establecer un método efectivo de comparación con otro conjunto infinito, haciendo que sus elementos desfilen emparejados en dos filas indias, exactamente igual que con los pollos (el término técnico en matemáticas para este emparejamiento se denomina correspondencia biyectiva).¡Dicho y hecho! Tomemos un conjunto infinito distinto, el de los números enteros o  , que como ya sabemos son los de la forma:
, que como ya sabemos son los de la forma:
 , que como ya sabemos son los de la forma:
, que como ya sabemos son los de la forma:........, -3, -2, -1, 0, 1, 2, 3, .........
Aparentemente uno podría pensar que este conjunto es evidentemente mayor que el de los números naturales, puesto que éstos están contenidos en él. Sin embargo, y contra toda intuición, vamos a "emparejar" ambos conjuntos y veremos que "ningún pollo queda descolgado":
Asociemos al número 0 (de los números enteros) el número 1 (de los números naturales). Al número 1 (de los números enteros) le corresponderá el número 2 (de los números naturales); al número -1 (de los números enteros) le corresponderá el número 3 (de los naturales), y así sucesivamente, como muestra la imagen siguiente:
Observamos que, por muchos pollos que hagamos desfilar por la puertecita del corral, todos seguirán emparejados, sin que ninguno de ellos pueda quedar descolgado. Acabamos de demostrar que ambos conjuntos tienen el mismo cardinal transfinito, que es, como ya hemos visto,  .
.
 .
.En este momento surgen algunas cuestiones, que resolveremos en un futuro artículo (si vemos que éste ha tenido aceptación):
- ¿Qué ocurre con los demás conjuntos de números: los racionales, los reales...?
- ¿Qué conjuntos infinitos son "más grandes" que el de los números naturales?
- ¿Hay más números pares positivos que números naturales?
- ¿Cómo es que un chamán de una tribu se maneja mejor con conjuntos infinitos que algunos catedráticos de matemáticas alemanes del S. XIX, a juzgar por la mala aceptación de las teorías de Cantor?
¡Hasta el infinito, y más allá!

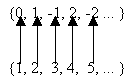
Felicidades, se entiende muy bien la idea de cardinal
ResponderEliminarEspero la continuación ;-)
Qué simpáticos los pollos, nos tenían engañados a todos y mientras ellos se guardaban su propia teoría de conjuntos...
ResponderEliminarYo también espero la continuación :)
Muy buen artículo ¿Tuvo continuación?!
ResponderEliminar